| Intitulé du problème soulevé. |
Messages traités |
Contributeurs |
Date |
Qui saurait calculer la distance horizontale
entre deux points (séparés d'environ 500 m) et dont
on possède les coordonnées ?
|
41 |
14 |
août 2017 |
Page mise à
jour le :
08-Nov-2019
|
Documents annexes (cliquer sur les documents pour
les agrandir)
|
| Doc.
1 :
Fichier tableur pour ce calcul (copie d'écran) |
Doc
2 :
Pythagore |
|
| |
|
|
| Avis divers |
|
| Facile, YAKA lire "Le P'tit Usania"
;-)
1. Le problème posé dans LPU n° 30 (févr.
2001) : http://usan.ffspeleo.fr/spip2129/spip.php?article184
2. Les éléments mathématiques de réponse
dans LPU n° 30 : http://usan.ffspeleo.fr/spip2129/spip.php?article189
3. La solution du problème pour ceux qui n'ont compris ou su
faire dans LPU n° 31 : http://usan.ffspeleo.fr/spip2129/spip.php?article193 |
En PJ un petit fichier
tableur et sans approximation (qu'ils disent). C’est
pas moi qui l’ai écrit mais c’est très pratique
en bartassant : calcul distance
.xls |
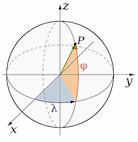
C’est la distance
orthodromique, soit la distance entre 2 points sur une sphère.
Voici le code en C# (prononcer "C dièse"
en français ou "C-sharp" en anglais) selon les normes
FAI (aviation civile). Pour de faibles distances "Pythagore"
reste largement suffisant. x0, y0 et x1, y1 sont les longitudes et
latitudes des points en degrés décimaux.
private static double
OrthodromicDistance(double x0, double y0, double x1, double y1)
{
x0 *= Math.PI /
180; y0 *= Math.PI / 180;
x1 *= Math.PI / 180; y1 *= Math.PI / 180;
return 6371000 * 2 * Math.Asin(Math.Sqrt(Math.Pow(Math.Sin((y0 - y1)
/ 2), 2) +
Math.Cos(y0) * Math.Cos(y1) * Math.Pow(Math.Sin((x0 - x1) / 2), 2)));
} |
Un papier et un crayon suffisent,
mais pour s'amuser à pas cher ou gratuitement il existe de
nombreux logiciels simples pour lycéens, collégiens,
et même aussi utilisables par des enfants du primaire :
Il y en a d'autres bien pires : MathLab, Mathematica
actuellement repris par WOLFRAM (c'est raide et uniquement en ligne
de commande, mais sans limites) ; ces derniers processeurs de calculs
sont lourds mais on peut trouver des vieux clous gratos. |
| Sinon pour faire les calculs avec des logiciels
libres : gNumerics,
multiplateforme, mais pas facile d'abord. |
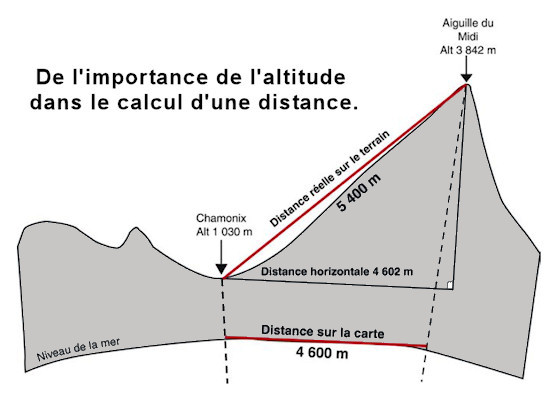
Sur 500 m à la surface de la terre quelle est déformation
sphérique ? Si on prend 40 000 km de périphérie
terrestre, 500 m = 1/80 000 de la circonférence. Calculer
la corde de l'arc sur 500 m, on peut sans passer par la trigonométrie
se dire qu'il y aura très très peu de différence
entre la longueur de l'arc et celle de la corde, donc effectivement
Pythagore suffit.
NDLR
: la "corde" est une droite qui jnoint deux points d'un
arc (voir ci-dessous)

|
Si on a les coordonnées dans un repère métrique
(Lambert ou UTM) c'est plus simple en effet. À nos
précisions c'est largement suffisant. Néanmoins ne
pas perdre de vue que le Lambert représente des mesures sur
la projection et que 1 km Lambert ne fait pas tout à fait
1 km terrain. C'est la conversion
degrés WGS84 <-> Lambert qui est chiante.

NDLR
: par rapport à la réalité, la projection transforme
les méridiens en droites concourantes (qui se rejoignent)
au point S
et les parallèles en cercles concentriques.
|
Variations, gags
et coups de gueule... |
Pas la peine de se mettre le
cerveau en clysopompe ; la plupart des sites de carto
offrent cette fonctionnalité, par exemple Geoportail.
C'est surtout pratique pour des distances ne dépassant pas
quelques kilomètres mais c'est souvent le cas pour nous. |
| Résumé du débat |
 Voilà donc deux formules
de calcul pour une surface plane (en négligeant la sphéricité
de la Terrre) et donc valables pour des distances relativement proches.
La première est la plus simple des deux car elle suppose que
les deux points sont à la même altitude (Z négligé).
La seconde un peu plus complexe tient compte de l'altitude de chacun
des deux points. Si vous n'êtes pas sur un Causse, préférez
donc la seconde.
Voilà donc deux formules
de calcul pour une surface plane (en négligeant la sphéricité
de la Terrre) et donc valables pour des distances relativement proches.
La première est la plus simple des deux car elle suppose que
les deux points sont à la même altitude (Z négligé).
La seconde un peu plus complexe tient compte de l'altitude de chacun
des deux points. Si vous n'êtes pas sur un Causse, préférez
donc la seconde.
- 1)
Soient deux points A et B dont on veut mesurer la distance.
Leurs coordonnées dans un repère orthonormé
classique [O,x,y] sont A : (Xa, Ya) et B : (Xb, Yb), le tout dans
un plan horizontal.
Distance [AB] = sqrt [ (Xa - Xb)² + (Ya - Yb)² ]
sqrt = racine carrée
CQFD
-
2
)
Soient deux points A et B dont on veut mesurer la distance. Leurs
coordonnées dans un repère orthonormé classique
[O,x,y,z] sont A : (xa, ya, za) et B : (xb, yb, zb) avec Oz vertical
orienté vers le haut (pour tenir compte de l'altitude du
point), Ox et Oy sont sur un plan horizontal (en gros, le plancher
des vaches).
Avec la relation de Chasle, le vecteur AB a pour coodonnées
: (xb - xa), (yb - ya), (zb - za)
Pour alléger la rédaction qui va suivre et faciliter
la lecture on va appeler "u, v, w" le triplet précédent
("u" mis pour (xb - xa) etc.).
D'après le théorème de Pythagore, AB ²
= u² + v² + w² ; on en déduit que la racine
carrée de (AB²) = AB = norme du Vecteur AB = sa "longueur"
pour les béotiens = distance entre A et B.
CQFD
|
Un
exemple avec la formule N°1
Calcul
de la distance (approximative) en mètres entre le Boulidou
de Cazilhac (point A) et l'Abîme de Rabanel
à Brissac (point B), les coordonnées utilisées
ici pour ces deux points sont en Lambert III métrique. A :
0709287 / (3)180878 et B : 708330 / (3)177065
NB : le chiffre "3" est entre
parenthèses car ce n'est pas un chiffre significatif de la
mesure de longueur projetée, c'est juste un préfixe
qui indique la zone III. Donc on ne s'en sert pas pour les calculs.
D²
= (709287 - 708330)² + (180878 - 177065)² = 957² +
3813² = 915 849 + 14 538 969 = 15 454 818 d'où D = 3 931,26
m
Le logiciel
de cartographie (qui calcule en orthodromie)
me donne 3 940 m : ce n'est déjà pas trop mal vu que
Rabanel fait bien plus de 8,74 m de diamètre...
Même
exemple avec la formule N°2
Il suffit
d'ajouter l'altitude, nous prendrons A : 166 m et B : 339 m
Donc D² devient 15 454 818 + (339 - 166)² = 15 454 818 +
27 556 = 15 482 374
D'où on calcule D = 3 934,76 m ce qui encore plus proche de
la valeur donnée par le logiciel (moins de 5 m d'écart
soit environ 0.1%) ! |
Compléments
d'information

|

Pour le cas où les liens de l'USAN ne fonctionneraient plus,
voici le condensé en .pdf des 3 textes parus dans le "Le
P'tit Usania" N°s 30 et 31 et cités plus haut : Problème
du mois USAN |
Sujets connexes :
|




 Relation de
Relation de 


